WebAssembly 向けのコンパイラを作ってみる

はじめに

結構前から wasm さわってみたいと思いつつ手を出せずにいたんですが 去年 C コンパイラを学んだりしてハードルが下がった感じがあって簡単なコンパイラ実装をやりはじめました。

まずは難しい機能は入れず C 言語から大分機能を落としたサブセットのコンパイラを作ることにしました。

リポジトリはこれです。

https://github.com/tkaaad97/wasm-experiment1

例として下のコードをコンパイルすると

void printf_i(string s, int a);

int add(int a, int b) {
    return a + b;
}

int main(int n, int b) {
    int a = 0;
    for (int i = 0; i < n; ++i) {
        a = add(a, b);
    }
    printf_i("a=%d\n", a);
    return a;
}

出力の wasm (テキスト形式) は下のようになります。

(module
  (import (;0;) "" "printf_i" (func (param i64 i32)))
  (type (;0;) (func (param i32 i32) (result i32)))
  (type (;1;) (func (param i32 i32) (result i32)))
  (func (;1;) (type 0) (param i32 i32) (result i32)
    local.get 0
    local.get 1
    i32.add
    return
    unreachable
  )
  (func (;2;) (type 1) (param i32 i32) (result i32)
    (local i32 i32)
    i32.const 0
    local.tee 2
    drop
    block
      i32.const 0
      local.tee 3
      drop
      loop
        local.get 3
        local.get 0
        i32.lt_s
        i32.eqz
        br_if 1
        local.get 2
        local.get 1
        call 1
        local.tee 2
        drop
        local.get 3
        i32.const 1
        i32.add
        local.tee 3
        drop
        br 0
      end
    end
    i64.const 12884901888
    local.get 2
    call 0
    local.get 2
    return
    unreachable
  )
  (export "memory" (memory 0))
  (export "add" (func 1))
  (export "main" (func 2))
  (memory (;0;) 1 10)
  (data (;0;) (i32.const 0) "a=%d\n\00")
)

WebAssembly 関連情報

wasm の仕様はここのようです。大体ここに必要なことは書かれているはずです。

webassembly.github.io

wasm の入門的な記事です。最初はこのあたりを読んだりしていました。

developer.mozilla.org

developer.mozilla.org

実行するときに wasmtime の C API を使いました。その他にもコマンドラインで色々試したりできます。

github.com

コンパイラ実装について

スタックマシン

前に C コンパイラ作成したときは x86-64 でやっていてこれはレジスタマシンでした。

wasm はスタックマシンなので色々と実装が変わってきます。

x86-64 向けの実装でもメモリ上のスタックは使っていたので、 スタックマシンではレジスタに動かす必要がなくなって実装が楽になるのかなと思ってましたが、 実装を進めるとちょっと勘違いしていたことがわかりました。

wasm のスタックはメモリ上のスタックとは違って操作がかなり制限されています。

例えば関数の引数とローカル変数には local.get という命令でアクセスできるんですが この引数には定数のインデックスしか渡せず何らかの計算をしたインデックスを使ったりできません。 配列をローカル変数としてスタック上配置したとしてもループで回してインデックスアクセスしたりできないわけです。

なので wasm 側のスタックとは別にメモリ上にアプリケーションがスタックとして使う領域を別に用意して使うことになるんじゃないかと思います。 C 言語と違ってポインタが無い言語ではまた実装違うかなという気もします。

今回実装した言語は機能を大幅にカットしていてポインタも配列も無いので 全部 wasm 側のスタックで済ませるということにしています。

四則演算

四則演算はそのままスタックに積んでいって計算すればいいので簡単です。

四則演算の例

1 + 2 * 3 - 4 / 5 + 6

wasm

    i32.const 1
    i32.const 2
    i32.const 3
    i32.mul
    i32.add
    i32.const 4
    i32.const 5
    i32.div_s
    i32.sub
    i32.const 6
    i32.add

関数

wasm にも関数の機能があって、これを C 言語の関数実装にも使えますが 先に触れたように引数とローカル変数におけるものが限られているのでちゃんと実装するには自前でメモリ上にスタックを作るなどする必要がありそうです。

関数には型が付きます。スタックから入力として使うデータの型とスタックに結果として残すデータの型です。 スタックに渡すデータの型や個数は実行前にチェックされて少し静的言語っぽい感じもしました。

関数の例

int add(int a, int b) {
    return a + b;
}

wasm の例

  (func (param i32 i32) (result i32)
    local.get 0
    local.get 1
    i32.add
  )

テキストフォーマットでは S 式のようにも書くことができます。

  (func (param i32 i32) (result i32)
    (i32.add (local.get 0) (local.get 1))
  )

if

wasm はジャンプ命令がなくてブロックがいくつかあります。

アセンブリだと普通ネストした構造はないですが wasm はこのあたり変わってて ブロックはプログラミング言語のようにネストした構造を作れます。

C 言語の if 文を実装するには wasm の if ブロックがそのまま使えます。

if 文の例

int min(int a, int b) {
    int c = 0;
    if (a < b) {
        c = a;
    } else {
        c = b;
    }
    return c;
}

wasm

  (func (param i32 i32) (result i32)
    (local i32)
    i32.const 0
    local.tee 2
    drop
    local.get 0
    local.get 1
    i32.lt_s
    if
      local.get 0
      local.tee 2
      drop
    else
      local.get 1
      local.tee 2
      drop
    end
    local.get 2
  )

この例だとパラメーターも結果も無いので省略されていますがブロックにも関数と同じように型が付きます。

関数内で if ブロックを使って return しようとすると警告出てしまうことがありました。

警告がでるコード

  (func (param i32 i32) (result i32)
    local.get 0
    local.get 1
    i32.lt_s
    if
      local.get 0
      return
    else
      local.get 1
      return
    end
  )

wat2wasm の警告

error: type mismatch in implicit return, expected [i32] but got []

こういう場合は unreachable を入れるといいようです。

  (func (param i32 i32) (result i32)
    local.get 0
    local.get 1
    i32.lt_s
    if
      local.get 0
      return
    else
      local.get 1
      return
    end
    unreachable
  )

for

for 文 は loop ブロックと br, br_if を使って作れます。

br と br_if は break と似てますが loop ブロックに使う場合は continue のような挙動になるようです。

loop ブロックの参考

qiita.com

for 文の例

    int a = 0;
    for (int i = 0; i < 10; ++i) {
        a = a + i;
    }

生成された wasm

    i32.const 0
    local.tee 0
    drop
    block
      i32.const 0
      local.tee 1
      drop
      loop
        local.get 1
        i32.const 10
        i32.lt_s
        i32.eqz
        br_if 1
        local.get 0
        local.get 1
        i32.add
        local.tee 0
        drop
        local.get 1
        i32.const 1
        i32.add
        local.tee 1
        drop
        br 0
      end
    end

break 実装するときに wasm 側でどのブロックを抜けるのか知る必要があります。

例えば for の中に if があってそこで break 使う場合は二つ上のブロックを抜けるように br 2 とします。

この部分は wasm 生成する関数で今 break 使ったらどのブロック抜けるかというのを引数で渡す感じで実装しました。

文字列リテラル

data segment という機能でメモリ上に文字列データを配置することができます。

コードに持つ文字列リテラルの情報としてはメモリ上のオフセットとサイズを持っておけばいいので

i64.const にオフセットとサイズを 32bit づつにして定数として埋め込んでいます。

グローバル変数

グローバル変数も wasm 側で機能が用意されていてある程度はこれを使えるんですが C 言語の機能とはちょっと違っています。

配列や構造体、ポインタとして扱うデータなどはメモリ側に置くことになると思います。

wasm グローバル変数の初期化式には定数式しか使えないので

C 言語の機能を実装していくにはグローバル変数初期化用の関数を作ったりする必要がありそうです。

ホスト側の関数を呼ぶには

wasm の範囲では標準入出力やファイルを扱ったりできません。

かわりにホスト側の処理を呼び出すことができるような仕組みがあります。

wasmtime では C API が実装されていてホスト側の関数ポインタをモジュールの import として呼び出せるようになっています。

JavaScript 向けの処理系では wasm から JavaScript の関数を呼び出すような仕組みを持っています。

また WebAssembly System Interface (WASI) というのが提案されていて入出力やファイルシステムなどを扱うための インターフェースが定義されて色々なランタイムが実装されているようです。

WASI を使って実装された wasi-libc というのもあって C 言語で実装されたものを wasm にするときには必要になりそうです。

github.com

printf を呼ぶ

ホスト側の関数を呼べるので printf なども使えますが可変長引数の仕組みはないので 引数を変えてたくさん関数を import したりする必要があります。

それか引数もメモリ上に配置してホスト側で復元して呼び出すような感じにもできるかもしれません。

今回使ってないですが wasi-libc に printf もあるらしいです。

感想

関数があったりネストした構文があったりしてアセンブラよりかなりプログラミング言語に近く感じました。

wasm にコンパイルできる言語は色々あるので別に自分でコンパイラ書く必要はそんなにない気もしますが色々勉強になりました。

私が使いたいところとしては Web でなにか動かしたいというよりは、 例えばゲームやアプリで一部スクリプトやプラグインのようなものを動かすのに使えるかもと考えてました。

今回は大分実装を省略しましたが配列、構造体、メモリ上のスタック、コルーチン (難しそう) などそのうち実装してみたいと思いました。

ノーマルマップのあれこれ

この記事

もう大分前ですが3Dモデルを読み込んで OpenGL で表示するようなプログラムを書いていて ノーマルマップを適用するあたりがなかなか難しかったのでまとめておこうという内容です。 ノーマルマップを使ったシェーダーの計算の話などです。

法線ベクトルの影響

Blender でフラットシェーディングとスムーズシェーディングを切り替えて法線ベクトル表示してみます。

フラット

スムーズ

結構見た目が変わります、さらにノーマルマップを付けると違ってきます。

シェーダーで使う式は色々ありますが多くのものは拡散光と反射光それから環境光を足し合わせるような形になっています。 拡散光と反射光に法線ベクトルが影響します。 拡散光の場合は光の方向ベクトルと法線ベクトルが影響し、反射光の場合はカメラの向きも影響します。

このあたりが参考になりそうです。

www.opengl-tutorial.org

あと glTF の仕様では式やレファレンス実装がわかるので勉強しやすい気がします。

github.com

github.com

頂点属性

ベースカラーマップで必要な頂点属性は uv 座標のみですが、 ノーマルマップの場合は uv 座標、法線ベクトル、接ベクトルが必要になります。

ノーマルマップのテクスチャから uv 座標で取得した法線ベクトルは、接ベクトル空間でのベクトルなのでこれをグローバル座標系に変換する必要があります。 接ベクトル空間の座標軸は接ベクトル (tangent) 、従法線ベクトル (bitangent) 、法線ベクトル (normal) と呼ばれます。 従法線ベクトルは接ベクトルと法線ベクトルの外積から求められるので頂点属性には入ってません。

頂点属性から接ベクトルを省略して uv 座標から求める方法が使われることがあります。

https://github.com/KhronosGroup/glTF-Sample-Viewer/blob/2e6f9f1cfef04239cc8c8c403a5c49a242b1dc3f/src/shaders/pbr.frag#L142-L143

    vec3 t_ = (uv_dy.t * dFdx(v_Position) - uv_dx.t * dFdy(v_Position)) /
        (uv_dx.s * uv_dy.t - uv_dy.s * uv_dx.t);

このあたりの計算がそれなんですがこれがどうやって出てきたかすぐは分かりませんでした。 色々式をいじってみたところ次のような感じだと思われます。

接ベクトルを $\textbf{t} = ( t _ {x}, t _ {y}, t _ {z} )^{T} $ 、 従法線ベクトルを $\textbf{b} = (b _ {x}, b _ {y}, b _ {z}) ^ {T} $ とします。

uv 座標系の $u$ 軸と接ベクトルが平行、$v$ 軸と従法線ベクトルが平行になるように $\textbf{t}$ と $\textbf{b}$ を求めます。

$\textbf{t}$ と $\textbf{b}$ で作られる平面上の点 $(t, b)$ のグローバル座標系での位置座標は下のようにあらわせます。

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix} \begin{pmatrix} t \\ b \end{pmatrix}= \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

$u$ で偏微分すると

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}= \begin{pmatrix} \frac{\partial x}{\partial u} \\ \frac{\partial y}{\partial u} \\ \frac{\partial z}{\partial u} \end{pmatrix} $$

$v$ で偏微分すると

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix}= \begin{pmatrix} \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial v} \end{pmatrix} $$

$\textbf{t}$ と $\textbf{b}$ を偏微分であらあわせました。

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix} =\begin{pmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{pmatrix} $$

glsl には dFdx, dFdy というスクリーン座標での偏微分を計算する関数があるのでこれを使う形に書き換えます。

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix} \begin{pmatrix} \frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} \\ \frac{\partial v}{\partial X} & \frac{\partial v}{\partial Y} \end{pmatrix}= \begin{pmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{pmatrix} \begin{pmatrix} \frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} \\ \frac{\partial v}{\partial X} & \frac{\partial v}{\partial Y} \end{pmatrix} $$

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix} \begin{pmatrix} \frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} \\ \frac{\partial v}{\partial X} & \frac{\partial v}{\partial Y} \end{pmatrix}= \begin{pmatrix} \frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y} \\ \frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y} \\ \frac{\partial z}{\partial X} & \frac{\partial z}{\partial Y} \end{pmatrix} $$

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix}= \begin{pmatrix} \frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y} \\ \frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y} \\ \frac{\partial z}{\partial X} & \frac{\partial z}{\partial Y} \end{pmatrix} \begin{pmatrix} \frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} \\ \frac{\partial v}{\partial X} & \frac{\partial v}{\partial Y} \end{pmatrix}^{-1} $$

$$ \begin{pmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{pmatrix}= \frac{1}{\frac{\partial u}{\partial X} \frac{\partial v}{\partial Y} - \frac{\partial u}{\partial Y} \frac{\partial v}{\partial X}} \begin{pmatrix} \frac{\partial x}{\partial X} & \frac{\partial x}{\partial Y} \\ \frac{\partial y}{\partial X} & \frac{\partial y}{\partial Y} \\ \frac{\partial z}{\partial X} & \frac{\partial z}{\partial Y} \end{pmatrix} \begin{pmatrix} \frac{\partial v}{\partial X} & - \frac{\partial v}{\partial Y} \\ -\frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} \end{pmatrix} $$

シェーダーのコードでは $\textbf{b}$ の方が使われてないですが $\textbf{t}$ は同じ形に変形できました。

dFdx, dFdy は使わずに似た計算で求める場合もあるようです。

marupeke296.com

www.opengl-tutorial.org

ノーマルマップありのシェーダーでの計算の流れ

頂点シェーダー

頂点シェーダーからピクセルシェーダーに接ベクトル、従法線ベクトル、法線ベクトルが渡されます。 頂点シェーダーでは接ベクトル、従法線ベクトル、法線ベクトルに変形行列をかけて回転させます。 変形行列をかけるとき平行移動は考慮しないように注意します。

ピクセルシェーダ

頂点シェーダーからピクセルシェーダーに渡されるときに線形補間されてベクトルの長さや直交関係がずれてしまうので補正します。 接ベクトル、従法線ベクトル、法線ベクトルとノーマルマップから取得したベクトルから実際の法線ベクトルを求めます。 ライトとカメラの情報はユニフォームで渡して拡散光や反射光の計算を行い結果の色を出力します。

どの座標系で計算するか

接ベクトル空間で計算を行うようにして、頂点シェーダーでライトとカメラのベクトルを接ベクトル空間に変換することで計算量を減らすという方法があります。

ただライトを複数渡したい場合にはこのやり方ではちょっと書きにくくなってしまいます。ということでグローバル座標系で計算するというやり方をする場合もあります。

参考

marupeke296.com

www.opengl-tutorial.org

wgld.org

Blender で 3D モデルのテクスチャに効果をつける

この記事

Blender を少し前に使いはじめたものの自分でモデリングはまだやったことがありませんでした。

昨年末ぐらいから動画を見たりしてモデリングやテクスチャやスキニングのやり方などを勉強中です。

モデリング練習でいらすとやのイラストを元にモデルを作ってみてたのですが塗りの部分にノイズのような効果がかかっています。 Blender でこうしたテクスチャの効果をつけるのはどうやるのかなと思ってやってみたという内容です。

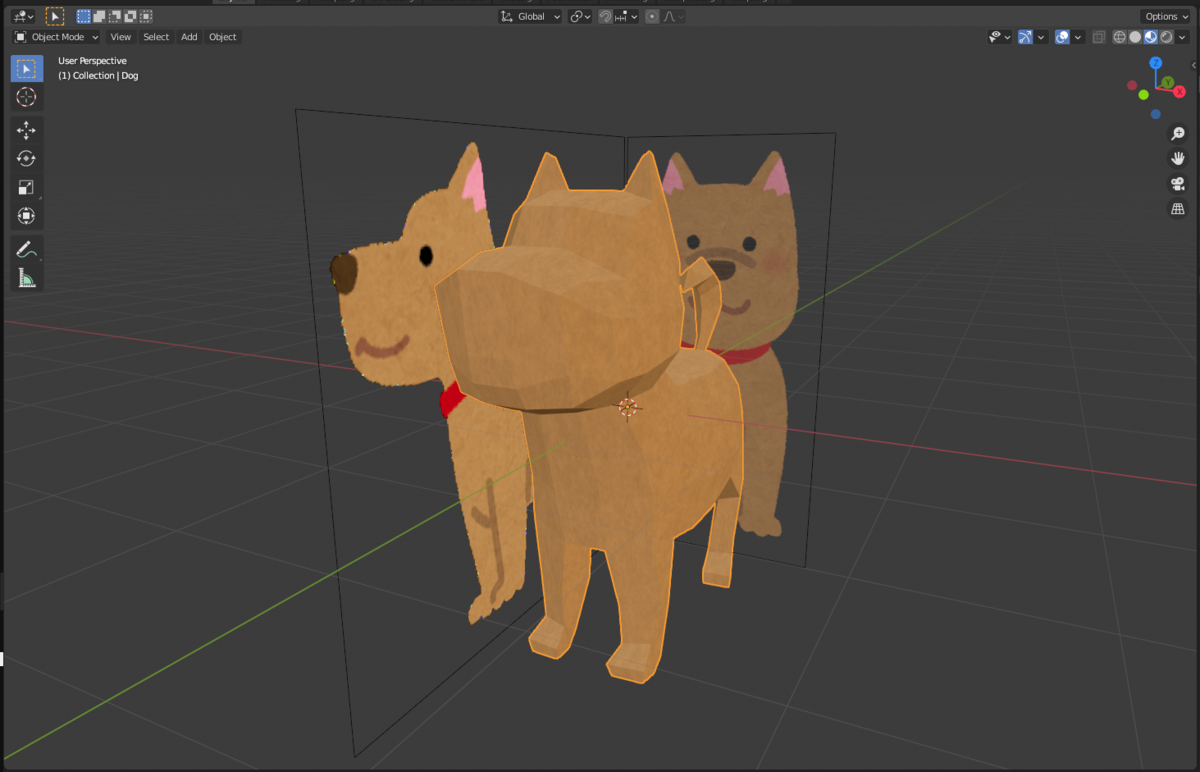
やり方

UV展開した状態のテクスチャ画像に効果を入れるの方が簡単だと思いますがこれだとシームの切れ目で不連続になってしまいます。

切れ目が問題にならないこともあるし、切れ目を目立たないように加工したりという方法もあると思いますがシェーダーノードでやってみました。

ノイズテクスチャやボロノイテクスチャを試してみると座標による関数になっていてシームでも連続となっていました。

ノイズテクスチャなどを使って合成していく感じで色々な効果が作れそうです。

docs.blender.org

ノイズテクスチャの実装はパーリンノイズのようです。

牛柄

ノイズテクスチャを使って閾値で白と黒で分けると牛柄のような感じにできました。

三毛

牛柄とあまり変わりませんが三色組み合わせると三毛柄にできます。

イラスト

いらすとやのような感じの効果をつけようとしたんですがちょっと違う感じになってしまいました。 ノーマルマップなども付けた方が紙のような雰囲気が出るかもしれません。

Cコンパイラの学習

この記事

「低レイヤを知りたい人のためのCコンパイラ作成入門」を読んでCコンパイラ書いてみた感想などです。

実際書いたコードはここに置いています。

github.com

テキスト

www.sigbus.info

このテキストは結構前に公開されたもののようでいろんな人がブログに書いたりしていて評判もよく実際学びやすいと思います。

難しいところはあまりなく読んでいて自分でもコンパイラ書けそうと思えてきます。

実習的な内容で読んで自分でコードを書きながら進めるところがよかったです。

まず最小構成でコード生成まで作って、小さいステップでテストを書きながら機能を追加していくというやり方も取り組みやすいと思いました。

何かコンパイラ的なものを作ろうとしてパーサーだけ作ってやめてしまったり、 途中の実装を無駄に凝ってすすめられなくなった経験が少なからずあるのでコンパイラ以外を作る場合にも参考にしたいなあと思いました。

後半は少し難しくなっていく気がしますが そこまで読み進めて理解できていれば解決できるということで意図的に細かいことは書かれていないのかもしれません。

言語の選択

セルフホストするところまでやるのが切りがよさそうなのでやっぱりC言語でやるのがいいのかなと思います。

セルフホストを気にしない場合は好きな言語で書いていいと思います。

私はC言語をあまり書きたくなかったのと、サンプルと同じように書いてしまうとコピペになってしまうかなという気がして Go で書いてました。

Go 使うことにしたのは前に少し触って書き方を忘れそうなので Go の学習のためというのもありました。

ただよく知っていて調べずに書ける言語で書いていく方がコンパイラを学ぶことに集中できると思います。

Go で書いてよかったところや書きにくかったところを挙げてみます。(私が Go の書き方を知らないせいもあるかもしれません。)

よかったところ

• 実装にあまり迷わなかった
• C言語に近い構文は大体ある
• スライスやマップが標準で使える
• type が別名ではなく別の型
• 関数から関数を返せる
• 無名関数を使える

書きにくく感じたところなど

• enumを簡単に文字列表示したい
• 整数型のmin, maxが欲しい
• スライスの比較が欲しい
• mapにキーがあるかどうか調べる関数が欲しい

式と文

最初は四則演算などの式だけをコンパイルして、スタックには一つ値が残った状態になるのでこれを pop するという実装になっていました。

if などを導入したときにこの部分でバグって少しはまっていました。 文の場合は式と違ってスタックに値が残らない場合があるので常に pop するとスタックがずれて壊れます。

結局 IsExpr 関数を作って式だったら pop するような感じで修正しました。

最適化は今回は全然手をつけられていないですが 簡単な実装だと無駄なレジスタ、スタックの移動が発生してしまうので最適化でこの辺の無駄をなくしたりするのかなと思いました。

Cの型のパース

Cの型のパースは難しく感じました。

ただこのテキストで扱う型は限られているので最初からそんなに完全な実装で無くてもよくてここで長く悩む必要はないです。

配列、関数、ポインタなど型の修飾が適用される順番が読む順番と逆にになっているところが難しいような気がします。

ここはパーサーの戻り値に型を受け取って型を返す関数を使うと実装しやすかったと思います。

色々な整数型の扱い

int だけでなく char が出てきて、レジスタも64ビットの他に32ビット、16ビット、8ビット版を扱うあたりが難しかったです。

変数からレジスタに読み込むところと、変数に書き込む部分だけ変数型とレジスタのタイプを気にしておけば 途中計算は int にして大体よさそうな気がするんですがいまいちこのあたり理解できてません。

ステップ28

ステップ28 でテストをC言語で書き直すというところがあります。

書く前はそこまでできるのかちょっと疑問に思いましたがやってみると意外にできて感動がありました。

ただここでテストに使う式や構文をどうやってテストに入れて実行したり表示したりするのか最初わかりませんでした。

ここは書かれてないけど多分プリプロセッサでマクロを使って書くということになると思います。

プリプロセッサは実装していないので gcc でプリプロセスのみを処理してからコンパイルしました。

Blender でスクリプトを使ってレンダリング

概要

tkaaad97.hatenablog.com

この記事で 3D モデルのアニメーションをレンダリングして連番の画像を生成するようなことをしていました。

このときは手動でやっていたんですがアニメーションが複数種類あって、種類によってはモデルの向きを変えてレンダリングするものもあったため 手動でこれを切り替えてレンダリングするのはかなり面倒でした。

Blender では Python スクリプトで色々な操作をすることができるらしく、こうした作業は自動でできそうなため調べてやってみたという内容です。

使った Blender ファイルの構造

Blender ファイル構造

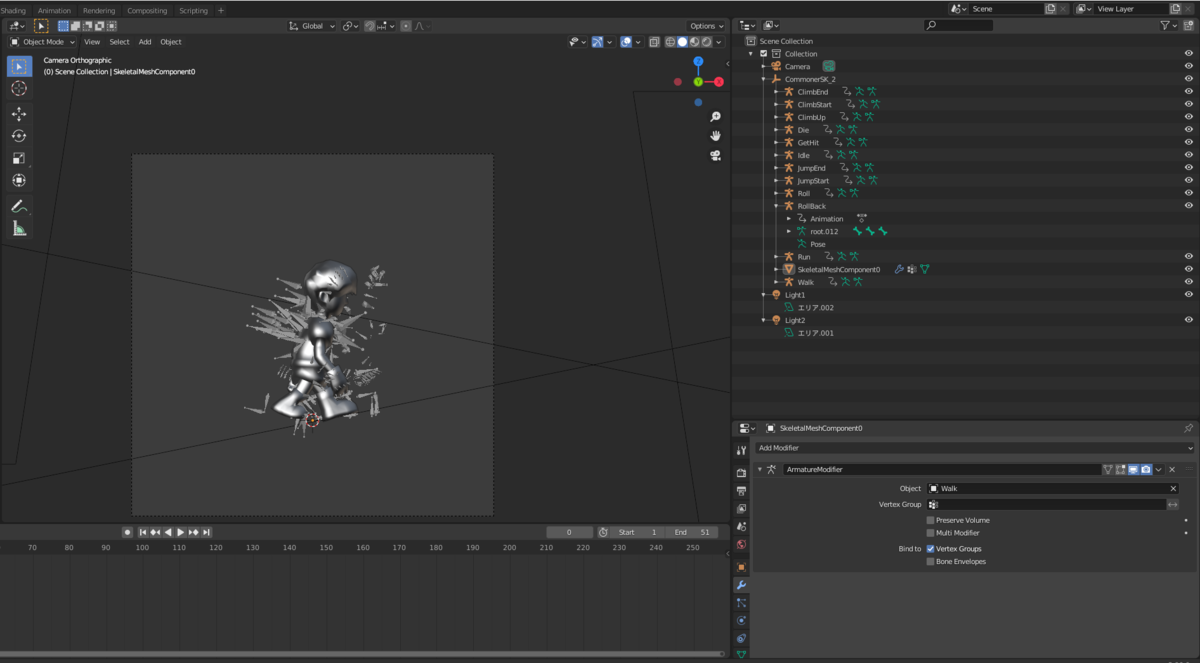
キャラクターの 3D モデルが一つあって、アニメーションはそれぞれ別々のアーマチュアについています。

アニメーションを切り替えるときはアーマチュアモディファイアを変更するというやり方をしています。

アーマチュア別々になっているのは UE4 からエクスポートしたモデルをインポートしているためこのようになっています。

(この構造もちょっと変なのでスクリプトでアニメーションを一つのアーマチュアにまとめることもできるかもしれません。)

レンダリングに使ったスクリプトの内容

かなりやっつけで書いたスクリプトなので全然汎用性はありません。 オブジェクトの構造や名前が違うと動きませんが参考にスクリプトを載せておきます。

このスクリプトでやっていることは下のような操作です。

• モデル側面配置でのレンダリング
  • ファイル出力パスの変更
  • シーンのフレーム数変更
  • 3D モデルの位置と向きを変更
  • アーマチュアモディファイアの変更
  • アニメーションレンダリング実行
• モデル背面配置でのレンダリング
  • ファイル出力パスの変更
  • シーンのフレーム数変更
  • 3D モデルの位置と向きを変更
  • アーマチュアモディファイアの変更
  • アニメーションレンダリング実行

import bpy
import math

def render_animation(armature_name):
    bpy.context.scene.render.filepath = "//out/" + armature_name + "/"
    bpy.context.scene.frame_start = int(bpy.data.objects[armature_name].animation_data.action.frame_range[0] + 0.5)
    bpy.context.scene.frame_end = int(bpy.data.objects[armature_name].animation_data.action.frame_range[1] + 0.5)
    bpy.context.view_layer.objects.active = bpy.context.scene.objects["CommonerSK_2"]
    bpy.context.object.location[0] = -0.16
    bpy.context.object.location[1] = 0.0
    bpy.context.object.location[2] = 0.0
    bpy.context.object.rotation_euler[0] = 0.0
    bpy.context.object.rotation_euler[1] = 0.0
    bpy.context.object.rotation_euler[2] = math.pi * 0.5
    bpy.context.view_layer.objects.active = bpy.context.scene.objects["SkeletalMeshComponent0"]
    bpy.context.object.modifiers["ArmatureModifier"].object = bpy.data.objects[armature_name]
    bpy.ops.render.render(animation=True)

def render_behind_animation(armature_name):
    bpy.context.scene.render.filepath = "//out/" + armature_name + "_Behind/"
    bpy.context.scene.frame_start = int(bpy.data.objects[armature_name].animation_data.action.frame_range[0] + 0.5)
    bpy.context.scene.frame_end = int(bpy.data.objects[armature_name].animation_data.action.frame_range[1] + 0.5)
    bpy.context.view_layer.objects.active = bpy.context.scene.objects["CommonerSK_2"]
    bpy.context.object.location[0] = 0.0
    bpy.context.object.location[1] = 0.0
    bpy.context.object.location[2] = 0.0
    bpy.context.object.rotation_euler[0] = 0.0
    bpy.context.object.rotation_euler[1] = 0.0
    bpy.context.object.rotation_euler[2] = math.pi
    bpy.context.view_layer.objects.active = bpy.context.scene.objects["SkeletalMeshComponent0"]
    bpy.context.object.modifiers["ArmatureModifier"].object = bpy.data.objects[armature_name]
    bpy.ops.render.render(animation=True)

armature_names = [
  "ClimbEnd",
  "ClimbStart",
  "ClimbUp",
  "Die",
  "GetHit",
  "Idle",
  "JumpEnd",
  "JumpStart",
  "Roll",
  "RollBack",
  "Run",
  "Walk"
]

behind_armature_names = [
  "ClimbEnd",
  "ClimbStart",
  "ClimbUp"
]

for armature_name in armature_names:
  render_animation(armature_name)

for armature_name in behind_armature_names:
  render_behind_animation(armature_name)

CLI で実行

スクリプト実行は Blender 実行中に Scripting タブでもできますが、CLI から Blender を起動せずに実行することもできます。

オプションの渡し方がいまいちわかってないですが、下のような感じで実行できました。

blender --background -noaudio Model.blend --python render.py

CLI のマニュアルはこれのようです。

docs.blender.org

やりたい操作に対応する API の探し方

docs.blender.org

最初は API ドキュメントから探そうとしてたんですが量が多すぎてここから検索して探すというのは結構難しいです。

Blender を手動で操作した後に Scripting タブを開いて履歴を見ると対応する操作がわかるので、これを参考にするというのがやりやすそうでした。

このキャプチャ画像のように左下あたりに出ています。

Scripting タブ

FFI のあれこれ

はじめに

少し前に FFI を使って Haskell から C++ の処理を呼び出すというのをやっていてなかなか大変だったのでこれについて書いておきます。

私がわからなくて調べたことなどあまり整理されてない雑多な内容になります。

FFI の情報

参考になりそうなページを貼っておきます。

wiki.haskell.org

xtech.nikkei.com

book.realworldhaskell.org

www.haskell.org

downloads.haskell.org

FFI を使ったところ

OpenGL であれこれ表示したりするコードを書いていて glTF をロードして3Dモデルを表示するというのをやっていました。 glTF で頂点データを圧縮することができる draco という拡張があります。 draco 拡張はどうも圧縮アルゴリズムが仕様としてあるわけではなくて draco 拡張を使う場合には draco ライブラリの関数を呼び出して頂点データをデコードする必要があるようです。

draco ライブラリは C++ で書かれていてこれを Haskell から呼び出すのには FFI が必要となりました。

実際の作業としては下のようなことをしましたが慣れないのもあってなかなか大変でした。

• draco ライブラリから呼び出す必要がある処理を見つける
• C言語でラッパーを作成
• Haskell から呼び出す部分の実装
• package.yaml の修正
• CI でビルドできるようにする

FFI で C++ 呼ぶ場合

Haskell からC言語の関数をインポートするのに foreign import ccall というのを使います。

(ccall の部分は呼び出し規約にあたるようで他に cplusplus とか jvm とかもあるようですが ghc には多分実装されてません。)

インポートしたC言語の関数は IO として使えて引数を渡して、戻り値を受け取ることができますが使える型には制限があります。

使える型はこのあたりに書かれてました。

https://hackage.haskell.org/package/base-4.14.0.0/docs/Foreign-Ptr.html#g:2

• the argument types are marshallable foreign types, i.e. Char, Int, Double, Float, Bool, Int8, Int16, Int32, Int64, Word8, Word16, Word32, Word64, Ptr a, FunPtr a, StablePtr a or a renaming of any of these using newtype.
• the return type is either a marshallable foreign type or has the form IO t where t is a marshallable foreign type or ().

構造体やクラスは値のままでは扱えないのでポインターにして受け渡す必要があります。

C++ はそのまま使えないので C でラップして使います。以下のものが必要になると思います。

• new でインスタンスを生成する関数
• delete でインスタンスを破棄する関数
• インスタンスと引数を受け取ってメンバ関数を呼び出す関数

それから C++ を使う場合はプロジェクトの設定で libstdc++ をリンクしたり cxx-options で C++ 用のオプションを指定する必要があります。

リソースの管理

FFI で生成したポインタはそのままでは GC で勝手に破棄されたりはしません。

https://xtech.nikkei.com/it/article/COLUMN/20080902/313965/

こちらに解説されているように newForeignPtr で Ptr から ForeignPtr を作って GC で回収されるときに破棄用の関数を呼ばせることができます。

https://qiita.com/tanakh/items/81fc1a0d9ae0af3865cb#with%E7%B3%BB%E9%96%A2%E6%95%B0

使い終わったらすぐに破棄する場合はこちらの記事のように bracket を使って with 関数を作ってあつかうと例外が投げられた場合にもリークしないので便利です。

Setup.hs でビルドできないか

使ったことないですが Setup.hs に書くことでビルド時に色々な処理を実行させることができます。

これを使って FFI でリンクするライブラリを一緒にビルドできないかと考えつきました。

しかし FFI を使っている色々なライブラリを見てもそういうことをしているプロジェクトはほとんどありませんでした。

この理由はいくつか考えられる気がしますが色々な環境に対応してビルドするのが難しいというのが一つの理由かなと思います。

それからライブラリによっては環境にインストールされている共有ライブラリをリンクするのが望ましいからという場合もあると思います。

draco の場合は Setup.hs で頑張ればなんとかビルドできなくもない気がするんですが Windows など色々な環境対応をしようとするとやっぱり大変そうです。

ほぼ自分しか使わないしビルドが少し複雑になってもまあいいかということで

draco は別にビルドして stack に --extra-include-dirs と --extra-lib-dirs のオプションを指定するという感じにしています。

このあたりのオプションは stack.yaml でも指定できます。

ghc から使われるコンパイラなどの設定

ghc --info でコンパイラやリンカなどの設定が見れます。

ghc --print-libdir で表示されるディレクトリに settings というファイルがあってこれが設定ファイルのようです。

PIC

static ライブラリをビルドするときは普通は -fPIC のオプションは付けないらしいんですが ubuntu (18.04 と 20.04) で draco をビルドしてリンクして使おうとすると下のようなエラーが出てしまいました。

/usr/bin/ld.gold: エラー: /work/./third_party/draco/build/libdraco.a(kd_tree_attributes_decoder.cc.o): requires dynamic R_X86_64_PC32 reloc against 'stderr' which may overflow at runtime; recompile with -fPIC

Windows では -fPIC なしでも問題なくリンクできていました。 Windows 環境ではどうも gold ではなく ld が使われているようなのでリンカの違いによるかもしれません。 原因よく理解できてないですが -fPIC つけてビルドするとリンク成功したためビルド時には -fPIC つけるようにしています。

タイルマップ描画のメモ

はじめに

もうずいぶん前ですが Tiled Map Editor についてブログに少し書きました。

その後最近になって Tiled Map Editor で作ったマップを描画する部分を OpenGL で実装したりしていたためメモとして書いておきます。

描画の方法

タイルマップのデータを元にしてマス目状にタイルセットの画像を描画していくことになります。

基本的にはテクスチャを貼った三角形をたくさん表示できればいいはずです。

タイル1マスごとにドローコール呼び出したりすると処理に時間がかかってしまうのでまとめて描画するようにします。

大分基礎的なことなので詳しくは別の資料をみてもらった方がいいと思います。

下のページなどが参考になるかなと思います。

www.opengl-tutorial.org

描画順

タイルマップの種類によっては隣り合うタイルが重なりあっていることがあるので気を付ける必要があります。

デプスを使って制御することもできますが、頂点バッファを作るときに描画順に三角形をソートしておくという方法でも制御可能です。

デプスを使わなくてもいいようにしておくとパースペクティブで表示したりもできます (あまり必要ない気もしますが)。

下はパースペクティブで表示してみた画像です。

タイルマップ

インスタンシング

インスタンシングという機能があって、これを使うと3Dモデルの位置や色などを変化させて大量に表示することができます。

インスタンシングについてこちらのページなどが参考になりそうです。

wgld.org

learnopengl.com

タイルマップ描画の場合は幅1で高さ1の四角形メッシュを位置、サイズ、UVを変えてたくさん表示するという感じになります。 インスタンシングで高速化するというよりは頂点バッファに持つデータの量を減らせて扱いやすくなるというのが利点かなと思います。

ちょっと検索してみたところタイルのインスタンシングだとパフォーマンスよくないという感じのことが書かれていました。

gamedev.stackexchange.com

しかし 2D ゲームで使うようなタイルマップのタイル数は多くないのでパフォーマンスで問題になることはそんなにないんじゃないかと思います。 モバイル端末の場合だと問題になったりインスタンシング自体対応していないということもあるかもしれません。

インスタンシングを使わない場合の頂点データは下のようになります。

• アトリビュート
  • 位置座標
  • UV座標
• 頂点数
  • タイル数 x 6

インスタンシングを使う場合の頂点データは下のようになります。

• アトリビュート
  • 位置座標
  • タイルサイズ
  • UV座標
  • UVサイズ
• 頂点数
  • タイル数と同じ

タイルサイズとUVサイズが全体で固定の場合はユニフォームに持つこともできます。 この他に先に触れた幅1で高さ1の四角形メッシュを表す頂点バッファも必要です。

アニメーション表示するには

タイルマップによってはアニメーションするものもあります。 例えば海や川など水の表現ではアニメーションが使われることが多いです。 アニメーションを表示するには一定時間でUV座標を更新してタイル画像を切り替えることになります。

UV座標は頂点バッファに入っているので頂点バッファを定期的に書き換えるというのがやり方としては一番簡単かなと思います。

この他にアニメーションで切り替わるタイルの情報をユニフォームバッファに保持して 頂点バッファにはこれを参照するインデックスを持たせるというようなやり方もできます。 この場合はユニフォームバッファのタイル情報だけを更新するため更新が少なくて済みます。